from binary to multiclass classification math behind machine learning models


  © 2024 borui. All rights reserved.

  This content may be freely reproduced, displayed, modified, or distributed with proper attribution to borui and a link to the article: 
  
  borui(2024-09-13 23:06:26 +0000). from binary to multiclass classification math behind machine learning models. https://borui/blog/2024-09-13-en-from-binary-to-multiclass-math-behind-ml-model.

@misc{
  borui2024,
  author = {borui},
  title = {from binary to multiclass classification math behind machine learning models},
  year = {2024},
  publisher = {borui's blog},
  journal = {borui's blog},
  url={https://borui/blog/2024-09-13-en-from-binary-to-multiclass-math-behind-ml-model}
}

The reason of this article is that during background studying for one of my research on fitting machine learning models to unbalanced data, I found no online material explained clear enough the math functions for both binary and multiclass classification and how are they related to one another; therefore, I hope to illustrate those in this article and help you have a better bigger picture about how the model is fitted through application of these functions.

output calculation: softmax and logistic function

Both are sigmoid functions.
Both are acting as link functions(AKA output layers in neural nets) that would map the input values to output values between interval $(0,1)$ , which is interpreted as possiblities during paramenter alignments of machine learning models.

softmax_demo1alt

Definition 1. The standard logistic function is defined as follows:

\displaystyle \sigma :\mathbb {R} \rightarrow (0,1)

\displaystyle \sigma (t)={\frac {e^{t}}{e^{t}+1}}={\frac {1}{1+e^{-t}}}

The logistic function is a sigmoid function, which takes any real input t, and outputs a value between zero and one.

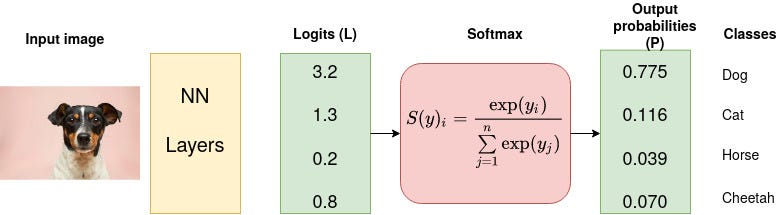
Prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval $( 0 , 1 )$ , and the components will add up to 1, so that they can be interpreted as probabilities. Furthermore, the larger input components will correspond to larger probabilities.

Definition 2. Formally, the standard (unit) softmax function σ : $\sigma \colon \mathbb {R} ^{K}\to (0,1)^{K}$ , where $K\geq 1$ , takes a vector z = $\mathbf {z} =(z_{1},\dotsc ,z_{K})\in \mathbb {R}^{K}$ and computes each component of vector $\sigma (\mathbf {z} )\in (0,1)^{K}$ with

\sigma (\mathbf {z}_{i})={\frac {e^{z_{i}}}{\sum _{j=1}^{K}e^{z_{j}}}}

https://en.wikipedia.org/wiki/Softmax_function

logistic loss can be seen as a special case of softmax

Therefore it is not hard to see that logistic function is a special case of softmax function, while vector $\vec{z}$ is a 2 dimension vector with potential values $\begin{bmatrix} t \\ 0 \end{bmatrix}$ .

The softmax function is hard to picture since it is multi variate, however the y intercept of the softmax function $\sigma(\mathbf {z}_{i})$ on the xoy coordinate system if for simplification of using one-hot vectors (vectors with value ${z}_{i}$ for one of its numbers and 0 for all the rest $\begin{bmatrix} {z}_{i} \\ \cdots \\ 0 \end{bmatrix}$ ) is:

\sigma (\mathbf {z}_{i}=0) = {\frac {e^{z_{i}}}{\sum _{j=1}^{K}e^{z_{j}}}}= {\frac {1}{K}}

loss calculation: cross entropy and logistic loss

The logistic loss can be combined into a single expression:

\ell _{k}=-y_{k}\ln p_{k}-(1-y_{k})\ln(1-p_{k})

📓 Note: The loss fucntion can take log of any base instead of ln here, same for coss entropy loss.

, where $y_k \in \{ 1,0 \}$ is whether the actual class is the selected one or the other. $p_k$ is the predicted probability of whether the class is the selected one.

or equivalently maximize the likelihood function itself, which is the probability that the given data set is produced by a particular logistic function:

L=\prod _{k:y_{k}=1}p_{k}\,\prod _{k:y_{k}=0}(1-p_{k})

https://en.wikipedia.org/wiki/Logistic_regression

This expression can be interpreted as a special case of cross-entropy expression like logistic function to softmax function as we mentioned earlier. If we generalize the class prediction into a 2 dimension vector $\begin{bmatrix} p_1 \\ p_2 \end{bmatrix}$ with $p_1$ and $p_2$ being the probability for two different class respectively, and the actual class being $\mathcal{X}=\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ or $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ respectively, then $\mathcal{X} = \begin{bmatrix} p_k \\ 1-p_k \end{bmatrix}$ is the predicted distribution for the 2 class by the model. Subsitute the values into cross entropy,

H(p,q)=- \sum_{x \in {\mathcal {X}}} p(x)\log{q(x)}

we will get the same result as with the logistic loss.

In fact, we will see why its named "cross" entropy by looking at the diagram of logistic loss function in a way that seperating two parts of the function to make them crossed to each other. binary_cross_entropy